[OTW] Write-up for the Krypton Wargame

---

The Krypton wargame is an online game offered by the OverTheWire community. This one is about cipher and cryptanalysis. Let’s get started !

Level 00 Solution

The host to which you need to connect for this challenge is krypton.labs.overthewire.org, on port 2222. The username is krypton1 and the password is… encoded with base64: S1JZUFRPTklTR1JFQVQ=

$ python3
Python 3.7.0 (default, Oct  2 2018, 09:20:07) 
[Clang 10.0.0 (clang-1000.11.45.2)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> import base64
>>> base64.decodestring(b"S1JZUFRPTklTR1JFQVQ=")

b'KRYPTONISGREAT'

Level 01 Solution

Using the previously found password, you can connect to the first level of this challenge. As per the instruction, the password for level 2 is in the file krypton2. It is encrypted using a simple rotation.

$ ssh krypton1@krypton.labs.overthewire.org -p 2222

krypton1@krypton:~$ cat /krypton/krypton1/krypton2
YRIRY GJB CNFFJBEQ EBGGRA

To solve this one, I just wrote a quick and dirty piece of code in Python to bruteforce the rotation. This script will rotate all the letter of the ciphertext and print the result.

import string

charset = string.ascii_uppercase
enc = "YRIRY GJB CNFFJBEQ EBGGRA"

for k in range(26):
    dec = ""
    for c in enc:
        if c in charset:
            idx = charset.find(c)
            idx += k
            if idx >= len(charset):
                idx -= len(charset)
            elif idx < 0:
                idx += len(charset)
            dec += charset[idx]
        else:
            dec = dec + c   
    print(dec)

After executing the code, the following line looked like english :

LEVEL TWO PASSWORD ROTTEN

Note: The substitution cipher used was in fact ROT13. You could also solve the challenge by using the following command echo "YRIRYGJBCNFFJBEQEBGGRA" | tr 'A-Za-z' 'N-ZA-Mn-za-m'.

Level 02 Solution

The password for level 3 is in the file krypton3. It is encrypted with Caesar’s Cipher, one of the simplest and most widely known substitution cipher.

$ ssh krypton2@krypton.labs.overthewire.org -p 2222

krypton2@krypton:~$ cat /krypton/krypton2/krypton3
OMQEMDUEQMEK

To solve this challenge, you can simply reuse the previous script to get all the shift possibilities.

import string

charset = string.ascii_uppercase
enc = "OMQEMDUEQMEK"

for k in range(26):
    dec = ""
    for c in enc:
        if c in charset:
            idx = charset.find(c)
            idx += k
            if idx >= len(charset):
                idx -= len(charset)
            elif idx < 0:
                idx += len(charset)
            dec += charset[idx]
        else:
            dec = dec + c   
    print(dec)

After executing the code, the following line looked like english :

CAESARISEASY

Level 03 Solution

The password to the next level is found in the file krypton4, it is encrypted using an unknown substitution cipher. However, we have access to 3 files (found1, found2, found3) and two important details :

• The files are in English
• They were produced from the same key as the password file

$ ssh krypton3@krypton.labs.overthewire.org -p 2222

krypton3@krypton:~$ cd /krypton/krypton3/
krypton3@krypton:/krypton/krypton3$ ls
HINT1  HINT2  README  found1  found2  found3  krypton4
krypton3@krypton:/krypton/krypton3$ cat krypton4 
KSVVW BGSJD SVSIS VXBMN YQUUK BNWCU ANMJS

The encrypted text is : KSVVW BGSJD SVSIS VXBMN YQUUK BNWCU ANMJS. If we do some frequency analysis on the files we have, we should be able to deduce the mapping used to encrypt the krypton4 file.

Here is a script to do frequency analysis in the found* files.

import string

# I did't filled the "msg" variable because it's quite long but
# you can get it by executing the following command :
# cat found* | sed 's/ //g' in the /krypton/krypton3/ folder

msg = "... snip ..."
letter_freq = {}

for c in string.ascii_uppercase:
    letter_freq[c] = 0

for l in msg:
    if l in string.ascii_uppercase:
        letter_freq[l] +=1 

s = [(k, letter_freq[k]) for k in sorted(letter_freq, key=letter_freq.get, reverse=True)]

print(s)

We obtain the following frequencies in the ciphertext files :

# [('S', 456), ('Q', 340), ('J', 301), ('U', 257), ('B', 246), ('N', 240), ('C', 227), 
# ('G', 227), ('D', 210), ('Z', 132), ('V', 130), ('W', 129), ('M', 86), ('Y', 84), 
# ('T', 75), ('X', 71), ('K', 67), ('E', 64), ('L', 60), ('A', 55), ('F', 28), ('I', 19), 
# ('O', 12), ('H', 4), ('R', 4), ('P', 2)]

So now, according to Wikipedia the letter frequency in the English language looks like that :

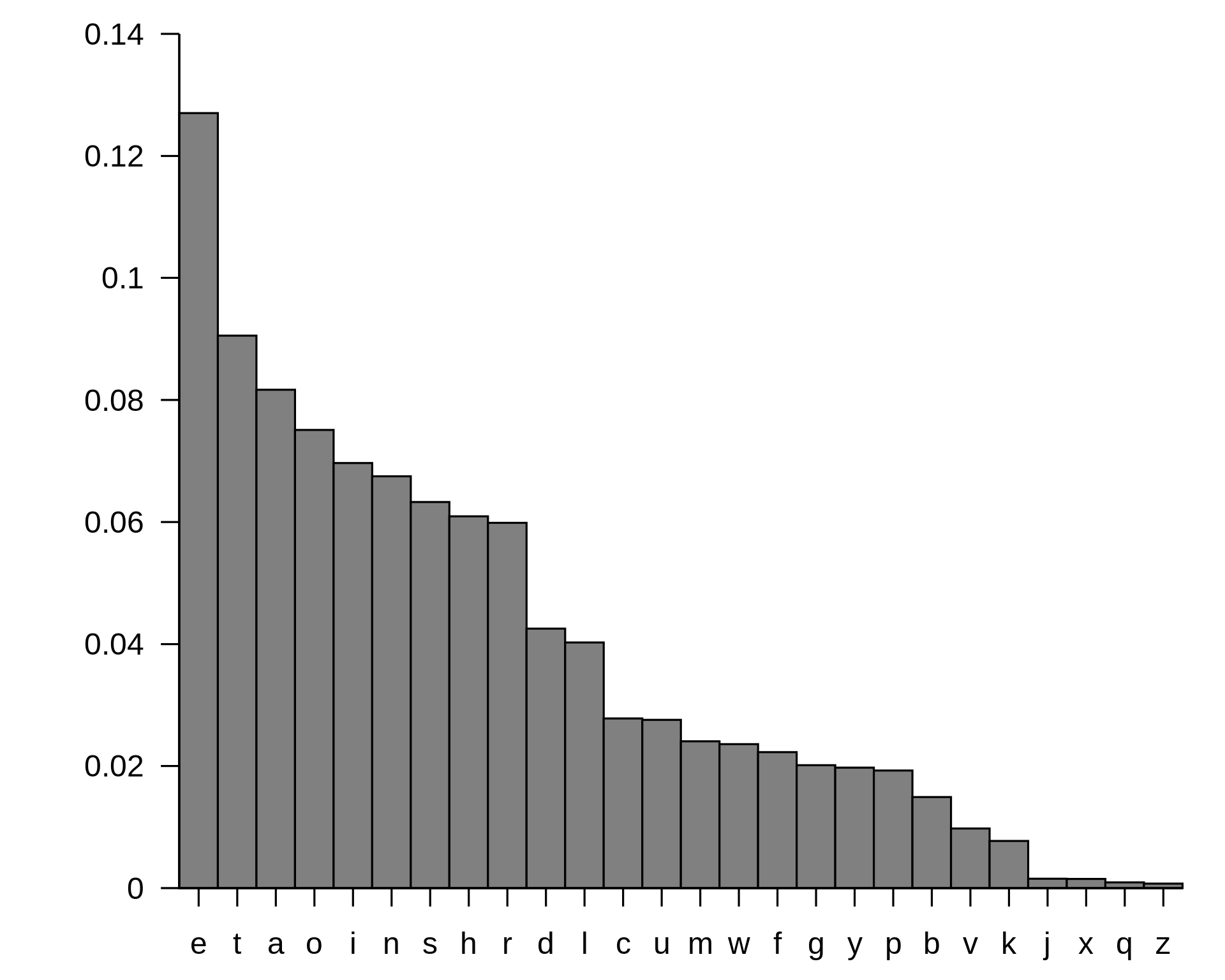
Now, let’s write a quick script to try to decipher the encrypted text by using the letter frequency used in the English language.

ciphertext = "KSVVWBGSJDSVSISVXBMNYQUUKBNWCUANMJS"
engligh_freq = "ETAOINSHRDLCUMWFGYPBVKJXQZ"
ciphert_freq = "SQJUBNCGDZVWMYTXKELAFIOHRP"

cleartext = ''
for l in ciphertext:
    i = ciphert_freq.index(l)
    cleartext += engligh_freq[i]

print(cleartext)

Hum… It does not seem to work :

GELLCIHEARELEKELFIUNMTOOGINCSOBNUAE

After some trial and error, I modified the original English frequency…

import string

ciphertext = "KSVVWBGSJDSVSISVXBMNYQUUKBNWCUANMJS"
#engligh_freq = "ETAOINSHRDLCUMWFGYPBVKJXQZ"
modified_freq = "EQTSORINHCLDUPMFWGYBKVXQJZ"
ciphert_freq = "SQJUBNCGDZVWMYTXKELAFIOHRP"

cleartext = ''
for l in ciphertext:
    i = ciphert_freq.index(l)
    cleartext += modified_freq[i]

print(cleartext)

It looks better now !

WELLDONETHELEVELFOURPQSSWORDISBRUTE

Level 04 Solution

So far we have worked with simple substitution ciphers. They have also been monoalphabetic, meaning using a fixed key, and giving a one to one mapping of plaintext (P) to ciphertext (C). Another type of substitution cipher is referred to as polyalphabetic, where one character of P may map to many, or all, possible ciphertext characters.

An example of a polyalphabetic cipher is called a Vigenère Cipher, which is used in this level. Here we have :

• 2 longer, english language messages (found1 and found2)
• The key length = 6
• The password file, krypton5, encrypted with the key used on found1 and found2

$ ssh krypton4@krypton.labs.overthewire.org -p 2222

krypton4@krypton:~$ cd /krypton/krypton4/
krypton4@krypton:/krypton/krypton4$ ls
HINT  README  found1  found2  krypton5
krypton4@krypton:/krypton/krypton4$ 
HCIKV RJOX

So, in this level “pure” frequency analysis won’t work very well, but there are ways around it. Here is a Vigenère square (or table):

With Vigenère, first you choose a key, like : SECURE and your cleartext : DONT WORRY BE HAPPY. If the message is longer than the key, you just repeat the key.

Then, the first letter of the plaintext, D, is paired with S, the first letter of the key. Therefore, row D and column S of the Vigenère square are used, namely V. Rinse and repeat until you encrypted the whole message.

DEC = DONTWORRYBEHAPPY
KEY = SECURESECURESECU
----------------------
ENC = VSPNNSJVAVVLSTRS

As you can see, frequency analysis on the whole message won’t work because each letter is encrypted with different parts of the key. However, we could do a frequency analysis on blocks of 6 chars (keylength) and treat them as 6 different mono-alphabetic ciphers.

Why ? Well, because every 6th character is encrypted the same way, with S in our example. Then, we essentially have 6 different messages that are normal Caesar shifts.

Let me show you :

ENC = VSPNNS JVAVVL STRS
DEC = DONTWO RRYBEH APPY
KEY = SECURE SECURE SECU

Here, 'V', 'J' and 'S' are the first letters of each encrypted block.
All of them have been encrypted with the letter 'S'.
If you apply the Caesar cipher with a shift of 8 you obtain :

'D', 'R' and 'A', the first letter of the each block of the cleartext !
You can apply the same formula to the second letter, third letter, etc.

Now, all we have to do is to write a script that :

• Create 6 Strings containing respectively all the 1st, 2nd, 3rd, 4th, 5th and 6th chars of a ciphertext
• Do every Caesar shifts on each of those strings
• Do frequency analysis on each of the Caesar shift results

Finally, if E is the most frequent letter of the string (because ‘E’ is the most frequent letter in the English language), we admit that we have the correct Caesar shift or cleartext so, we can recover the key.

Let’s recover the key !

import string

def split(key_length, ciphertext):
    res = []
    for x in range(key_length):
        tmp_str = ''
        for c in range(x, len(ciphertext), key_length):
            tmp_str += ciphertext[c]
        res.append(tmp_str)
    return res

def caesar(ciphertext, shift):
    charset = string.ascii_uppercase
    dec = ""
    for c in ciphertext:
        if c in charset:
            idx = charset.find(c)
            idx += shift
            if idx >= len(charset):
                idx -= len(charset)
            elif idx < 0:
                idx += len(charset)
            dec += charset[idx]
        else:
            dec = dec + c   
    return dec

def frequency(text):
    letter_freq = {}
    for c in string.ascii_uppercase:
        letter_freq[c] = 0
    for l in text:
        if l in string.ascii_uppercase:
            letter_freq[l] +=1 

    s = [(k, letter_freq[k]) for k in sorted(letter_freq, key=letter_freq.get, reverse=True)]
    return s

charset = string.ascii_uppercase
engligh_freq = "ETAOINSHRDLUCMWFYGPBVKXJQZ"
# Too long. Result of cat found1 | sed 's/ //g'
ciphertext = "... snip ..."
key_length = 6

data = split(key_length, ciphertext)
key = ''
for line in data:
    for shift in range(26):
        t = caesar(line, shift)
        if frequency(t)[0][0] == 'E':
            c = charset.find(line[0])
            c -= charset.find(t[0])
            c %= len(charset)
            key += charset[c]

print(key)

The result is FREKEY. And after decrypting the krypton5 file with the Vigenère square you obtain :

CLEARTEXT

Level 05 Solution

This level is the same as the previous one however, we don’t have the key length.

$ ssh krypton5@krypton.labs.overthewire.org -p 2222

krypton5@krypton:~$ cd /krypton/krypton5/
krypton5@krypton:/krypton/krypton5$ ls
README  found1  found2  found3  krypton6
krypton5@krypton:/krypton/krypton5$ cat krypton6 
BELOS Z

Here, I just used my previous script and tweaked the key size until I got the following result : XEYLENCTH. I just figured out that the key could be KEYLENGTH and it worked…

RANDOM

I’ve been lucky for this one. Normally, I would have used the Kasiski Examination to find the key length first and then, apply some frequency analysis.

Level 06 Solution

This is the last one ! Here, this is a stream cipher. A stream cipher attempts to create an on-the-fly random keystream to encrypt the incoming plaintext one byte at a time. Typically, the random key byte is xor’d with the plaintext to produce the ciphertext If the random keystream can be replicated at the recieving end, then a further xor will produce the plaintext once again.

In this challenge, we have a keyfile in our directory, however it is not readable. The binary encrypt6 is also available. It will read the keyfile and encrypt any message we want, using the key AND a random number. We get to perform a known ciphertext attack by introducing plaintext of our choice. The challenge here is not simple, but the random number generator is weak.

$ ssh krypton6@krypton.labs.overthewire.org -p 2222

krypton6@krypton:~$ cd /krypton/krypton6/
krypton6@krypton:/krypton/krypton6$ ls
HINT1  HINT2  README  encrypt6  keyfile.dat  krypton7  onetime
krypton6@krypton:/krypton/krypton6$ cat krypton7 
PNUKLYLWRQKGKBE

Fine. Let’s try to encrypt a cleartext of our choice.

krypton6@krypton:/krypton/krypton6$ python -c "print 'A'*100" > /tmp/plain.txt
krypton6@krypton:/krypton/krypton6$ ./encrypt6 /tmp/plain.txt /tmp/cipher.txt
krypton6@krypton:/krypton/krypton6$ cat /tmp/cipher.txt
EICTDGYIYZKTHNSIRFXYCPFUEOCKRNEICTDGYIYZKTHNSIRFXYCPFUEOCKRNEICTDGYIYZKTHNSIRFXYCPFUEOCKRNEICTDGYIYZ 

OMG ! That’s bad… You don’t see it ? Look closer…

EICTDGYIYZKTHNSIRFXYCPFUEOCKRN
EICTDGYIYZKTHNSIRFXYCPFUEOCKRN
EICTDGYIYZKTHNSIRFXYCPFUEOCKRN
EICTDGYIYZ

See ? Every 30 characters the pattern repeat itself. Let’s try another cleartext.

krypton6@krypton:/krypton/krypton6$ python -c "print 'B'*100" > /tmp/plain2.txt
krypton6@krypton:/krypton/krypton6$ ./encrypt6 /tmp/plain2.txt /tmp/cipher2.txt
krypton6@krypton:/krypton/krypton6$ cat /tmp/cipher2.txt
FJDUEHZJZALUIOTJSGYZDQGVFPDLSOFJDUEHZJZALUIOTJSGYZDQGVFPDLSOFJDUEHZJZALUIOTJSGYZDQGVFPDLSOFJDUEHZJZA

Interesting, same pattern but, every characters are increased by one…

FJDUEHZJZALUIOTJSGYZDQGVFPDLSO
FJDUEHZJZALUIOTJSGYZDQGVFPDLSO
FJDUEHZJZALUIOTJSGYZDQGVFPDLSO
FJDUEHZJZA

Now, let’s try to recover the ciphertext…

crypt = 'EICTDGYIYZKTHNSIRFXYCPFUEOCKRN'
ciphertext = "PNUKLYLWRQKGKBE"

for i in range(len(ciphertext)):
    k = ord(ciphertext[i]) - ord(crypt[i])
    if k < 0: k += 26
    k += ord('A')
    print(chr(k), end='')

And we got the following result :

LFSRISNOTRANDOM

Awesome, you did it ! I hope you had fun :)